Previous Month | RSS/XML | Current | Next Month

WEBLOG

September 29th, 2025 (Permalink)

The Zebra Fallacy?

There's an old saying that when you hear hoofbeats, you should expect a horse, not a zebra¹. This aphorism appears to have come from the context of disease diagnosis, where it's meant to draw an analogy between diagnosis and inferring what kind of hoofed animal made the sounds heard, so the symptoms of the disease are likened to the sounds made and the disease itself to the kind of animal making those sounds. The moral that is supposed to be drawn is that when the same symptoms―hoofbeats―could be explained by more than one disease―a horse or a zebra―the diagnostician should diagnose the more common and familiar disease―the horse. Here is how a textbook on pediatric health care explains it:

The analogy of hearing hoofbeats and looking for a zebra versus a horse holds true for all medical signs and symptoms. Both zebras and horses may cause similar-sounding hoofbeats, but a look out the window is more likely to reveal a horse than a zebra.²

This maxim probably originated here in North America as it wouldn't make sense in Africa where the zebra may be more common than the horse, so that African doctors should expect the zebra. In contrast, horses are common in North America but zebras are found only in zoos, so that if you hear hoofbeats here it could be a zebra escaped from a zoo, but it's far more likely to be a horse.

Now, the maxim is not just for medical diagnosis and hoofbeat identification, but can be applied to many other situations. For instance, suppose that you get a quick glimpse of a large woodpecker in the woods of Arkansas: is it a pileated woodpecker or an ivory-billed woodpecker? The pileated is common to forested areas of the eastern part of the continent³, whereas the ivory-billed is probably extinct⁴. While it may not be impossible that you saw an ivory-billed, it's far more likely that you saw the similar-looking pileated.

The zebra maxim instructs us to expect the more common cause when the evidence does not favor the less common one, but what happens when we violate it? I suggest naming the error of violating the maxim "the zebra fallacy" after this adage. This name should help to remind us of the nature of the mistake, namely, adopting a less probable hypothesis to explain evidence that can be explained equally well by a more probable one.

The maxim is not just a rule of thumb, but an application of a theorem of the calculus of probabilities―see the Technical Appendix, below. In English, the theorem says that if two hypotheses explain the same evidence equally well, then that evidence has no effect on their relative probabilities, that is, the more probable hypothesis remains more probable.

Pseudoscience and conspiracy theories often use the zebra fallacy since they tend to select the less likely hypothesis to explain a phenomena. For instance, consider the notorious case of the Cottingley fairies: I won't rehearse the historical details since I've done so elsewhere⁵, but the two competing hypotheses were that, first, two young girls repeatedly photographed fairies in their garden that no one else saw and, second, that the girls had faked the photos and lied about it. Both hypotheses explain the evidence⁶, and the second is far more a priori likely than the first.

I'm seriously considering adding an entry for this fallacy to the files and Taxonomy, but I'd like to have at least a few explicit examples in addition to the woodpeckers and the fairies before I do so.

Technical Appendix: For those familiar with probability theory, here's the theorem underlying and supporting the zebra maxim, together with a proof given in the axiom system for logical probability calculus⁷.

The Zebra Theorem: If P(h1) > P(h2) & P(e|h1) = P(e|h2) & P(e) > 0, then P(h1|e) > P(h2|e)⁸.

Proof: Assume the hypothesis of the theorem. We need to show that P(h1|e) > P(h2|e).

P(h1|e) = P(h1)P(e|h1)/P(e) (by Bayes' Theorem) = P(h1)P(e|h2)/P(e) (by hypothesis) = P(h1) × P(e|h2)/P(e) (by algebra).

P(h2|e) = P(h2)P(e|h2)/P(e) (by Bayes' Theorem) = P(h2) × P(e|h2)/P(e) (by algebra).

Let P(e|h2)/P(e) = c, then we have proven that P(h1|e) = P(h1)c and P(h2|e) = P(h2)c.

∴ P(h1|e) > P(h2|e), by hypothesis and the following fact about inequalities⁹:
If a > b then ac > bc, where all of a, b, and c > 0.⊣

This theorem can be easily generalized to any finite number of competing hypotheses that explain the evidence equally well by applying it pairwise to every pair of hypotheses. It also can be generalized to any relationship of equality or inequality between the hypotheses. Such a generalized theorem says that evidence that is equally well explained by competing hypotheses does not change the relationship between those hypotheses' probabilities, whether of equality or inequality.

Notes:

↑ For a thorough discussion of what is known about the origin of the saying, see: "Quote Origin: When You Hear Hoofbeats Look for Horses Not Zebras", Quote Investigator, 11/26/2017. To make a long story short: no one knows for sure who created it.
↑ Catherine DeAngelis, Basic Pediatrics for the Primary Health Care Provider (1975), p. 172. Found via Google Books.
↑ "Pileated Woodpecker", All About Birds, accessed: 9/28/2025.
↑ "Ivory-billed Woodpecker", All About Birds, accessed: 9/28/2025.
↑ See: Fairy Tale, 2/6/2013.
↑ Actually, I'm giving the fairy hypothesis more credit than it deserves since the photos look fake, which means that the evidence actually supports the more likely hypothesis.
↑ For the axioms, see: Probabilistic Fallacy.
↑ In this theorem, h1 and h2 are the two hypotheses being compared, P(h1) and P(h2) represent the "prior" probabilities of the hypotheses, and the first conjunct of the antecedent of the theorem tells us that the prior probability of h1 is greater than that of h2. "e" stands for the evidence, and P(e|h) is the probability of the evidence given the hypothesis h, which represents the degree to which h explains e. So, the second conjunct of the antecedent tells us that h1 and h2 explain e equally well. The third conjunct of the antecedent is included simply because we will need in the proof to divide by the probability of the evidence, P(e), so it can't be zero. Moreover, if the probability of e were zero then it would be false and, thus, worthless as evidence of anything. Finally, the consequent says that the posterior probability of h1 given the evidence is greater than that of h2.
↑ Paul Sanders, Elementary Mathematics: A Logical Approach (1963), p. 100, Postulate XIb.

September 17th, 2025 (Permalink)

Lesson in Logic 22: Polysyllogisms and Euler Diagrams ^*

As discussed in lesson 20, the technique of turning a polysyllogism into a chain of categorical syllogisms can show the validity of an argument that a single standard Venn diagram could not handle. However, the circles of Leonhard Euler, introduced in the previous lesson, can be used to show validity in a single diagram. 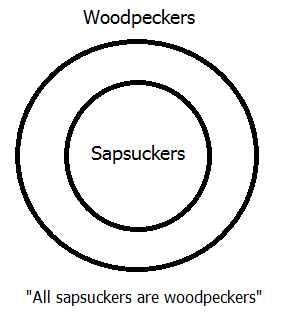To see how this method works, let's apply it to the polysyllogism used as an example in lesson 19: All sapsuckers are woodpeckers

All sapsuckers are woodpeckers.
All woodpeckers are birds.
All birds are animals.
Therefore, all sapsuckers are animals.

There are three premisses, all of which are A-type statements, that need to be represented in our diagram. Recall from the previous lesson that Euler represented such statements by drawing a circle for the subject class inside a circle for the predicate class. In this case, it doesn't matter which premiss you start with, so lets begin at the beginning with the first premiss. "Sapsuckers" is the subject class and "woodpeckers" is the predicate class, so we represent the first premiss as shown above. Euler diagram 1

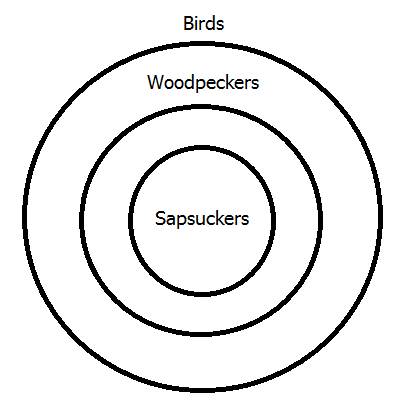
Turning now to the second premiss, remember that in diagramming arguments the premisses are all represented on a single diagram, whether Venn or Euler. So, we need to show on the same diagram that the class of woodpeckers is contained within the class of birds. Since we already have a circle for woodpeckers, all that we need is a new circle for birds, and the former should be inside the latter as shown above.

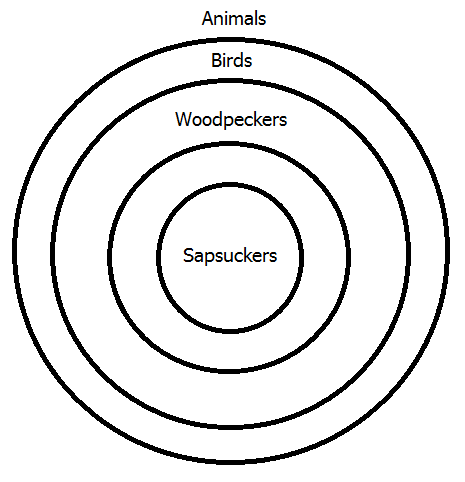
Notice that the second diagram shows that the class of sapsuckers is a subclass of the class of birds―in other words, all sapsuckers are birds―which was the intermediate conclusion in the chain argument given to show this polysyllogism valid in lesson 19. The final step is to diagram the third and last premiss, which means placing the "Birds" circle within a circle representing all animals, as shown above.

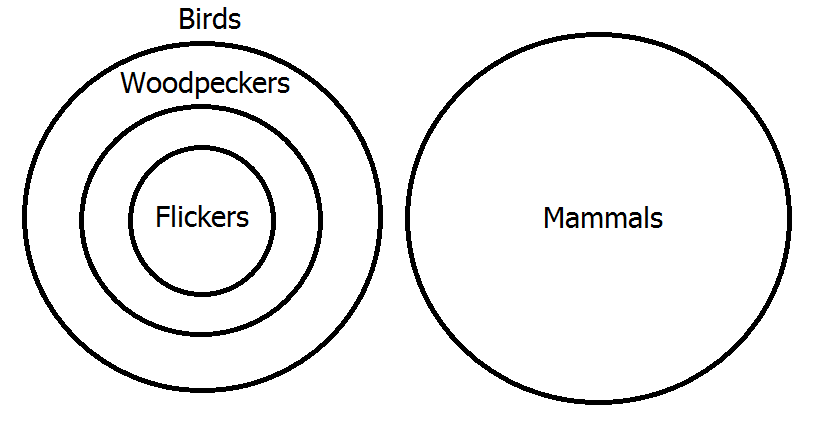
The finished diagram clearly shows the logical relationships between the four classes, and you can see that the conclusion is true and, therefore, the argument is valid. In my opinion, this is far easier and more perspicuous than the chain argument of lesson 19. However, that's just one example, so let's look at another example from that lesson, this one including an E-type statement: Euler diagram 2

All flickers are woodpeckers.
No birds are mammals.
All woodpeckers are birds.
Therefore, no flickers are mammals.

Since we already know how to diagram A statements, let's consider premisses 1 and 3 first. The result of diagramming both will look like the second diagram above but with "flickers" in place of "sapsuckers". Now, to diagram the second premiss, we must add a circle representing mammals that is disjoint from the circle for birds; the result looks as shown. Again, you can see from the diagram that the conclusion of the argument is true―that no flickers are mammals―and, thus, that the argument is valid, since it shows that the classes of flickers and mammals are disjoint.

As I mentioned in the previous lesson, Euler's diagram's for particular statements―that is, I- and O-type statements―are what led to Venn's different approach to using circles to represent classes. In the next lesson, we'll see how to combine Venn's technique with Euler's to diagram polysyllogisms with particular premisses. In the meantime, here's a polysyllogism to practice diagramming:

Exercise: Use an Euler diagram to show the following polysyllogism valid:

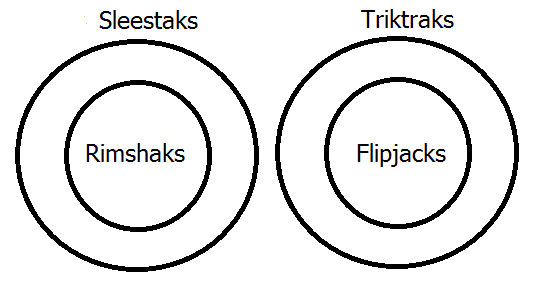
All rimshaks are sleestaks.
No sleestaks are triktraks.
All flipjaks are triktraks.
Therefore, no flipjaks are rimshaks.

^* ↑ For previous lessons in this series, see the navigation panel to your right.

September 6th, 2025 (Permalink)

Crack the Combination XI ^*

The combination of a lock is four digits long and each digit is unique, that is, each occurs only once in the combination. The following are some incorrect combinations.

8 1 7 4: One digit is correct but is in the wrong position.
5 4 9 6: No digits are correct.
7 4 3 1: Two digits are correct but neither is in the right position.
4 1 9 0: One digit is correct and in the right position.

Can you determine the correct combination from the above clues?

^* ↑ Previous "Crack the Combination" puzzles: I, II, III, IV, V, VI, VII, VIII, IX, X

September 4th, 2025 (Permalink)

What's New?

The Fallacy Files Taxonomy of logical fallacies is―that is, there's a brand new version of it: just click on "Taxonomy" to your upper right. In case you're interested, the old versions are still available from the following page, where you can also read about how you might make use of the taxonomy: The History of the Taxonomy. Check it out!

September 1st, 2025 (Permalink)

To err is human but to really foul things up requires artificial intelligence

I'm recommending the following article largely because I've never seen one on bad charts in The Washington Post before. Almost all of the charts shown are bad in ways I've also never seen before, so I won't have anything to say about most of them. What's interesting is not so much the charts themselves as that such atrocious charts were presented at all, especially from the artificial intelligence companies who did so. How did it happen? Don't those companies have any natural intelligences working for them?

Shira Ovide, "The AI industry is awash in hype, hyperbole and horrible charts", The Washington Post, 8/12/2025. The writing in this article is cloying―it sounds as if it were written by a teenager―but I've edited out the worst of it below, so proceed to the article itself at your own risk.
The mockery about "chart crimes"…nearly overshadowed the technology upgrades announced by two artificial intelligence start-ups. During a demonstration Thursday of ChatGPT's newest version, GPT-5, the company showed a visual in which it appeared 52.8 percent was a larger number than 69.1 percent, which, in turn, was somehow equal to 30.8 percent.

Ironically, at this point the article is interrupted by a Post promotion that reads: "Get concise answers to your questions. Try Ask The Post AI."
… Several more times in the demonstration, ChatGPT parent company OpenAI showed confusing or dubious graphics, including others in which a smaller number appeared visually larger than an actually bigger number…. Conspiracy theories started that AI generated the botched data visuals. (An OpenAI employee apologized for the "unintentional chart crime," and CEO Sam Altman said on Reddit that staff messed up charts in rushing to get their work done. Asked for further comment, OpenAI referred to Altman's Reddit remarks.)

Like the so-called lab leak theory, they aren't "conspiracy theories" but reasonable hypotheses to explain what is otherwise hard to understand. How were such "horrible" charts not only made but shown to the public? The claim by Altman isn't plausible, since the kind of errors made in OpenAI's charts are not the kind made by human beings. Certain types of errors in chartmaking are common to inexperienced people, and some types are common to those with experience and intent to deceive, but these were not of either type. Thus, it seems plausible that they were created using AI, though that doesn't explain why some human being didn't sanity check them. Perhaps the people who work there have too much faith in their own product.
… Also last week, the start-up Anthropic showed two bars comparing the accuracy rates of current and previous generations of its AI chatbot, Claude. …

The y-axis of the bar chart in question¹ does not start at zero percent, a common type of graphical distortion often used to exaggerate a difference². Moreover, there's no indication in the chart itself that it has been truncated so that you have to look at the y-axis scale to discover it. In the rare case when it's permissible to truncate a chart, it's obligatory to include a break in the scale to alert the reader to the truncation³, though this particular chart is not a rare case.
Anthropic has a motive to exaggerate the two percentage point gain in accuracy between Claude Opus 4 and Opus 4.1. This is an all-too-human "error", as opposed to the bizarre ones made by the OpenAI charts. If I find out that Anthropic's bar chart was generated by AI, I'll be more impressed by Claude's ability to imitate humanity than GPT-5's.
Jessica Dai, a PhD student at the University of California at Berkeley's AI research lab, said her big beef with the Anthropic chart was the "hypocrisy," not the off-base scale. The company has previously prodded researchers evaluating AI effectiveness to include what are called confidence intervals, or a range of expected values if a data study is repeated many times.

This is good advice.
Dai wasn't sure that's the right approach but also said that Anthropic didn't even follow its own recommendation. If Anthropic had, Dai said, it might have wiped out statistical evidence of an accuracy difference between old and new versions of Claude. …

Another all-too-human reason for the omission.
[T]o some data experts and AI specialists, the chart crimes are a symptom of an AI industry that regularly wields fuzzy numbers to stoke hype and score bragging points against rivals. …
Big technology companies and start-ups love charts that appear to show impressive growth in sales or other business goals but that have no disclosed scale that reveal the numbers behind those graphics. … To the companies, these charts offer a glimpse of their success without overexposing their finances. …

This explanation works for Anthropic's chart but not for those put out by OpenAI. Moreover, it's true of every industry.
By the way, I agree whole-heartedly with the following comment by charting guru Alberto Cairo:
He wasn't irked only about the basic arithmetic abuses. Cairo also was dubious about OpenAI's and Anthropic's use of graphs for two or three numbers that people could understand without any charts. "Sometimes a chart doesn't really add anything," he said. …
Cairo pointed to research that may help explain why companies gravitate to charts: They ooze authority and objectivity, and people may be more likely to trust the information.

Pointing to some uncited "research" as support also oozes "authority and objectivity, and people may be more likely to trust the information". Luckily, in this case, common sense and experience support Cairo's claim.
To [Dai] and some other AI specialists with whom I spoke, misguided charts may point to a tendency in the industry to use confidently expressed but unverified data to boast about the technology or bash competitors.
The Post previously found that AI detection companies claiming to be up to 99 percent accurate had largely untested capabilities. Meta was mocked this spring for apparently gaming its AI to boost the company's standings in a technology scoreboard. … "Just because you put a number on it, that's supposed to be more rigorous and more real," Dai said. "It's all over this industry."

It's all over all industry.
Kyle Orland, "LLMs' 'simulated reasoning' abilities are a 'brittle mirage,' researchers find", Ars Technica, 8/11/2025
In recent months, the AI industry has started moving toward so-called simulated reasoning models that use a "chain of thought" [COT] process to work through tricky problems in multiple logical steps. At the same time, recent research has cast doubt on whether those models have even a basic understanding of general logical concepts or an accurate grasp of their own "thought process." Similar research shows that these "reasoning" models can often produce incoherent, logically unsound answers when questions include irrelevant clauses or deviate even slightly from common templates found in their training data.

My experience with testing the ability of the allegedly artificially intelligent chatbots to solve simple logic puzzles is similar⁴.
In a recent pre-print paper, researchers from the University of Arizona summarize this existing work as "suggest[ing] that LLMs [Large Language Models] are not principled reasoners but rather sophisticated simulators of reasoning-like text." To pull on that thread, the researchers created a carefully controlled LLM environment in an attempt to measure just how well chain-of-thought reasoning works when presented with "out of domain" logical problems that don't match the specific logical patterns found in their training data.

In case you don't know, "pre-print" means that this paper has not been peer-reviewed or published yet, so take it with a dose of salts.
The results suggest that the seemingly large performance leaps made by chain-of-thought models are "largely a brittle mirage" that "become[s] fragile and prone to failure even under moderate distribution shifts," the researchers write. "Rather than demonstrating a true understanding of text, CoT reasoning under task transformations appears to reflect a replication of patterns learned during training." …
As the researchers hypothesized, these basic models started to fail catastrophically when asked to generalize novel sets of transformations that were not directly demonstrated in the training data. While the models would often try to generalize new logical rules based on similar patterns in the training data, this would quite often lead to the model laying out "correct reasoning paths, yet incorrect answer[s]." In other cases, the LLM would sometimes stumble onto correct answers paired with "unfaithful reasoning paths" that didn't follow logically.
"Rather than demonstrating a true understanding of text, CoT reasoning under task transformations appears to reflect a replication of patterns learned during training," the researchers write. …
Rather than showing the capability for generalized logical inference, these chain-of-thought models are "a sophisticated form of structured pattern matching" that "degrades significantly" when pushed even slightly outside of its training distribution, the researchers write. Further, the ability of these models to generate "fluent nonsense" creates "a false aura of dependability" that does not stand up to a careful audit.
As such, the researchers warn heavily against "equating [chain-of-thought]-style output with human thinking" especially in "high-stakes domains like medicine, finance, or legal analysis." Current tests and benchmarks should prioritize tasks that fall outside of any training set to probe for these kinds of errors, while future models will need to move beyond "surface-level pattern recognition to exhibit deeper inferential competence," they write.

I'm far from an expert on this kind of AI, but my impression is that it imitates writing about reasoning rather than actually reasoning.